SVreX (Forum Supporter) said:
In reply to MadScientistMatt :
If Monty ever opened a door with the car, there would be no need to switch. Unless you happened to like the other goat better! (and the odds would ALWAYS remain 1 out of 3).
Monty always reveals a goat. That's the "trick".
But does Monty have an option to not open any doors whatsoever? If so, does he only open a door with a goat when he wants to sucker you into switching?

mtn
MegaDork
7/1/21 7:56 a.m.
MadScientistMatt said:
SVreX (Forum Supporter) said:
In reply to MadScientistMatt :
If Monty ever opened a door with the car, there would be no need to switch. Unless you happened to like the other goat better! (and the odds would ALWAYS remain 1 out of 3).
Monty always reveals a goat. That's the "trick".
But does Monty have an option to not open any doors whatsoever? If so, does he only open a door with a goat when he wants to sucker you into switching?
It doesn't matter. It is very simple: If he opens a door, switch. If he doesn't open a door, switch or don't switch, you have the same odds on any of the available doors.
Like Mtn said.
The trick in this is that people think the odds have not changed.
We all understand that the initial choice is a 33% chance. Correct.
We THINK that once one option has been eliminated, the odds shift to 50/50. But that's not true. The odds are now 67% in favor of switching, 33% in favor of staying.
The reason the odds change is because Monty's elimination is not random.
The explanation that helped me understand the problem was the 100-door version. You pick a door, then Monty opens 98 doors leaving one closed door. Should you switch? At that point, it makes more sense to me that there is a 99% or 99/100 chance that the closed door has the car, not a 50% chance.
Reframe the scenario. You're not picking a door that you think has the car behind it. You're picking a door that you think *doesn't* have the car behind it. You are deciding ahead of time, "I want *not* this door."
Monty then says, "Of the two doors you think the car *might* be behind, it is definitely *not* behind this other door."
The logical conclusion then is, "If it's not behind the door I picked, and it's not behind the door that Monty revealed, it is behind the only remaining door."
You have a 2/3 chance of picking a door that the car *isn't* behind.
In reply to Beer Baron :
Wow. That was almost Donald Rumsfeld-ish! 

Hive,
Here's the experimental setup I used yesterday:

The engineer (um, contestant) stands on the opposite side of the labels which I use to keep track of which cups have a sports car and which cups have a goat.
If they pick the sports car in the first row, they can proceed to the second row...if they pick the sports car in the second row, they can proceed to the third and final round.
If they switch every time after I reveal a goat, they have ~30% chance of winning the sports car (.67 X .67 X .67)...if they stay with their original choice every time after I reveal a goat, they have ~3.6% chance of winning the sports car (.33 X .33 X .33).
I ask everyone to say what they think the best strategy is (stay, go, or it doesn't matter) before we run the experiment. Typically about half say it doesn't matter and I assign them to either stay or go to get a 50/50 split of strategies.
Don't laugh but I actually have something of a sentimental attachment to those cups. In 2019 alone, they flew with me to Penang Malaysia, Puerto Rico, Costa Rica, Atlanta, and eight trips to various locations in Minnesota.
Something that hasn't come up in this thread is the interesting story of Marilyn vos Savant who, with her highest ever recorded I.Q. of 228, explained why switching was advantageous in her weekly newspaper column "Ask Marilyn" and was publicly ripped to shreds by multiple professors of mathematics and statistics until she provided proof that she was correct.

mtn
MegaDork
7/1/21 12:19 p.m.
My google fu is weak. I seem to recall us having this same discussion a few times in the past, and wanted to read the responses but can't find it.
RX, I like that setup! Never thought to take it farther, other than to have more doors.

In reply to mtn :
Here are the CDF's for the two strategies assuming six participants go (first table) and six participants stay (second table)

The probability of at least one person winning for each strategy is one minus the probability of nobody winning.
So, with this setup, we've got a solid 88.24% chance of at least one goer winning (1-0.1177) and only a 19.75% chance of at least one stayer winning (1-0.8025).
Here's a typical example of one of my experimental outcomes (names removed to protect the innocent)...
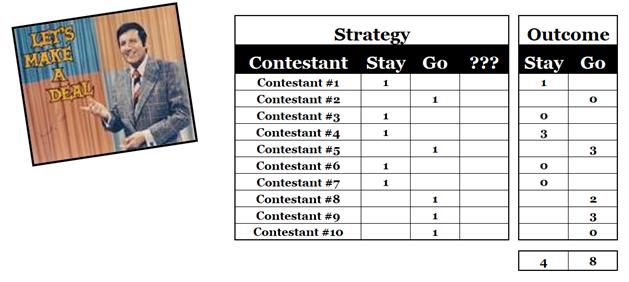
The "???" column is used to capture participants that think it doesn't matter if they go or stay and as I said, I move them into one or the other strategy to get a 50/50 balance before starting the experiment.
Notice that I don't just record if they win the sports car, instead I capture their success on each trail to provide better resolution in the data.
Added later...
I think we should take a moment to appreciate what a fantastically diverse group of people we have here on GRM.
MTN posts "hey, anybody know about the Monty Hall paradox" and 71 minutes later, I come back with "I'll actually be demonstrating the principle to a dozen engineers in two hours".
I just think it's cool how between us, there isn't much we don't know about.

Jay_W
SuperDork
7/1/21 12:47 p.m.
Keith Tanner said:
This is obviously a thought experiment. We never built a Miata with an LS7.
Obviously an oversight that needs correcting!
In reply to RX Reven' :
You stole my thunder. I was going to say, whatever you do, don't ask Marilyn...




































