mtn
MegaDork
1/26/10 5:51 p.m.
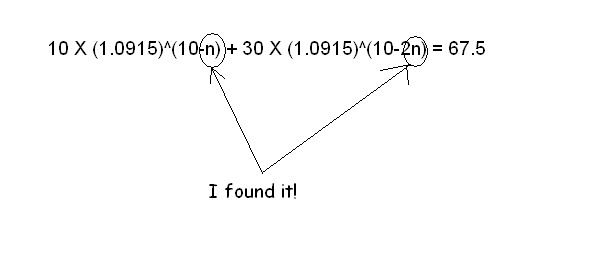
10 X (1.0915)^(10-n) + 30 X (1.0915)^(10-2n) = 67.5
I feel like this should be really easy, but I can't figure it out. I've been spoiled for the past few years using calculators that can figure anything out, and now I'm stuck--no calculators allowed. I can do complex integration, complex derivations, figure out interest in more ways than you ever knew existed. And yet I can't figure this damn equation out. Anyone got any idea? I'm almost afraid to ask because I know I'm going to hit myself when I see how easy it is.
Thanks everyone

cwh
PowerDork
1/26/10 5:57 p.m.
Whay are them upside down v things for?
to the power of aka Carot used to separate the base and exponent in a power expression
Are we trying to find "n" ? or 96?

mtn
MegaDork
1/26/10 6:02 p.m.
yeah, the carrot is to signify power.
5 squared is 5 to the second power is 5^2 is 25.

mtn
MegaDork
1/26/10 6:03 p.m.
Grtechguy wrote:
Are we trying to find "n" ? or 96?
Sorry, we're trying to find n. I just edited the original post, it all equals 67.5.
so this thread?
http://www.actuarialoutpost.com/actuarial_discussion_forum/showthread.php?t=129319

mtn
MegaDork
1/26/10 6:04 p.m.
Grtechguy wrote:
so this thread?
http://www.actuarialoutpost.com/actuarial_discussion_forum/showthread.php?t=129319
Thats the equation, out of the same book, with the same answer. I guess that I never thought of googling it. Thanks!
but can you explain it to us?

mtn
MegaDork
1/26/10 6:19 p.m.
Grtechguy wrote:
but can you explain it to us?
The problem said:
Joe deposits 10 today and another 30 in five years into a fund paying simple interest of 11% per year. Tina will make the same two deposits, but the 10 will be deposited n years from today and the 30 will be deposited 2n years from today. Tina's deposits earn and effective annual rate of 9.15%. At the end of 10 years, the accumulated amount of Tina's deposits equals the accumulated amount of Joe's deposits. Calculate n.
So to figure this out, we have to figure out Joe's Accumulated Value (AV) using simple interest at a rate of 11%. This is the easy part, and it comes out to 67.5
Next, we come up with the equations to figure out Tina's AV. We know the AV, but not the time... which comes out to 10-n for the first deposit, and 10-2n for the second. This gives us the equation
10 X (1.0915)^(10-n) + 30 X (1.0915)^(10-2n) = 67.5
This is the hard part. The thread that you posted above (I just bookmarked that website) explains it as well as is possible--write it out and its easier to understand--takes some difficult algebra to figure it out though. It uses some exponential tricks that I forgot ever existed back in highschool, or never learned. Actually, I had already done everything there but got lost in it and couldn't simplify it to the point needed.
You can turn that equation above into this:
10 (1.0915)^10(1.0915^(-n)) + 30 (1.0915)^(10)(1.0915^(-2n)) = 67.5
Which doesn't look too pretty, so you need to use a substitution, let x = 1.0915^(-n)
Write it out again, and its recognizable as a quadratic. Almost. I wouldn't have realized it was if the thread didn't tell me, but at least I could figure it out.
hence the superdork status

mtn
MegaDork
1/26/10 9:55 p.m.
Somehow I don't think that my professor would accept that.

mtn
MegaDork
1/26/10 10:11 p.m.
Tommy, you're a math "nerd" in high school, right? Try these pickup lines. Might work better for you than they did for me.
If you're X^2, then I want to be X^3/3 so I could be the area beneath your curve.
I wish i were your derivative; that way i could lie tangent to your curves.
Tommy, here's math philosophy:
The optimist says the glass is half full.
The pessimist says the glass is half empty.
The engineer says the glass is twice as big as it should be.

kcmoken
New Reader
1/27/10 8:22 a.m.
n=2.326, this seemed like an interesting problem so I got myself a cup of coffee, jammed a quick model, and used an interative process to hone in on n. I figure four significant digits is good enough.
I then check on the thread, they only left it at 2.3. I see now that the question is how to solve this problem on a test, so my iterative model is probably not the best solution. Except with a calulator, the iterative process would still be pretty quick, although maybe not to four significant digits. I certainly need to brush up on significant digits.
Punch that sucker in my 20 year old HP calculator and it would take about 2 seconds.

mtn
MegaDork
1/27/10 12:20 p.m.
kcmoken wrote:
n=2.326, this seemed like an interesting problem so I got myself a cup of coffee, jammed a quick model, and used an interative process to hone in on n. I figure four significant digits is good enough.
I then check on the thread, they only left it at 2.3. I see now that the question is how to solve this problem on a test, so my iterative model is probably not the best solution. Except with a calulator, the iterative process would still be pretty quick, although maybe not to four significant digits. I certainly need to brush up on significant digits.
Its in years, they don't get too picky with it for this.
Would you mind my asking how you did it? Was it similar to the way described in the thread above? And are you an actuary?
Dr. Hess wrote:
Punch that sucker in my 20 year old HP calculator and it would take about 2 seconds.
I have two calculators that could do it as well... I actually had figured out the answer long before I posted this. The problem is that I need to show work, and I'm preparing for the FM actuarial exam. They only allow certain calculators on the exam so I need to figure out the answer using what I am allowed.

kcmoken
New Reader
1/27/10 2:06 p.m.
I used an iterative process;
1) starting anywhere, I simply set n=0 and solved the equation, 99.
2) I set n=1, solved the equation to get a feel for what magnitude of n might be, 85.
3) Try again with 2, 72.38.
4) Close here, try again with n=3, 62.01 - clearly 2<n<3.
5) Now lets try solving for n=2.5, 66.98, clearly 2<n<2.5.
6) Next try 2.25, 69.62, clearly 2.25<n<2.5.
7) You can zero in on the answer very quickly with just a calculator.
I am not an actuary, I am an injuneer.

mtn
MegaDork
1/27/10 3:17 p.m.
kcmoken wrote:
I used an iterative process;
1) starting anywhere, I simply set n=0 and solved the equation, 99.
2) I set n=1, solved the equation to get a feel for what magnitude of n might be, 85.
3) Try again with 2, 72.38.
4) Close here, try again with n=3, 62.01 - clearly 2<n<3.
5) Now lets try solving for n=2.5, 66.98, clearly 2<n<2.5.
6) Next try 2.25, 69.62, clearly 2.25<n<2.5.
7) You can zero in on the answer very quickly with just a calculator.
I am not an actuary, I am an injuneer.
Wow. That is a lot smarter and easier than the way I was doing it.
That's how my calculator solves it with the SOLVE button.
I remember from my Calculus for Dummies course (AKA "Business Calculus") that there were some equations that just could not be solved, and they involved variables inside those upside down v things, whatever, and the solution was as kcmoken describes.